| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 데이터 해저드
- DNN Accelerator
- Pyverilog 튜토리얼
- gcc 컴파일
- Pyverilog 실행
- 클럭 게이팅
- Makefile compile
- CDC
- CLOCK GATING
- pygraphviz 설치 오류
- makefile
- 컨벌루션 연산
- 딥러닝 가속기
- linux c++ 컴파일
- gpgpu-sim
- linux c 컴파일
- pyverilog 설치 오류
- DNN 가속기
- Pyverilog 설치
- CUDA
- 남산업힐
- Design DNN Accelerator
- Data HAzard
- AMBA
- 대구 반도체 설계기업 특화
- linux makefile 작성
- Pyvrilog tutorial
- 이진수 곱셈 알고리즘
- systolic array
- pytest-pythonpath 설치 오류
- Today
- Total
오늘은 맑음
Study note : Efficient Processing of Deep Neural Networks(4) 본문
5.4 ARCHITEECTUREAL TECHNIQUES FOR EXPLOITING DATA REUSE
5.4.1 Temporal reuse
Temporal reuse는 PE에서 같은 데이터를 한 번 이상 사용할 때를 의미합니다.
Temporal reuse는 실제로 원본 데이터를 가지고 있는 memory인 Source level보다 더 작은 메모리인 Intermediate level을 사용해서 구현할 수 있습니다.

위의 그림 (d)와 같이 source mem으로 부터 데이터를 Intermediate L1 Mem으로 가져온 후 consumer에서 반복적으로 사용을 하게 되면 지속적으로 Source Mem에 접근할 필요 없이 바로 intermediate L1 Mem에서 데이터를 재사용할 수 있으므로 전체적으로 energy cost를 줄일 수 있습니다.
Intermediate L1 Mem는 Source Mem보다 작기 때문에 지속적으로 데이터를 교체해주어야 하는데, 데이터는 reuse distance에 의해 교체됩니다.
그림 (b)는 reuse distance가 4입니다. Intermediate L1 Mem은 1이지만 reuse distance가 더 큰 상황이죠. 따라서 Intermediate L1 Mem의 데이터는 (a)의 연산을 수행하면서 모든 MAC연산마다 데이터가 교체되는 것을 볼 수 있습니다. 이렇게 되면 Temporal reuse를 전혀 활용하지 못하는 상황이 되는 거죠.
하지만 그림 (c)의 경우 Intermediate L1 Mem의 크기와 같이 reuse distance가 1입니다. 이 때에는 데이터가 4번 연산될 때 마다 한 번씩 교체되는 것을 볼 수 있습니다.
따라서 reuse distance는 Intermediate L1 Mem의 크기에 따라 제한됩니다.
만약 reuse distance를 늘리기 위해 Intermediate L1 Mem을 크게 잡고 사용할 수도 있습니다. 이렇게 되면 한 번에 메모리로 부터 읽는 데이터가 많아져 메모리 접근 비용이 증가하게 됩니다. 따라서 reuse distance를 늘리는 것 보다 MAC연산기의 연산 순서를 변경하여 reuse distance를 줄이는 방향이 좋다고 할 수 있습니다.
Intermediate L1 Mem과 같이 memory hierarchy를 늘려 여러 번에 걸쳐 tamporal reuse를 사용할 수도 있습니다.
이렇게 하면 점점 작은 메모리를 이용해서 temporal reuse를 사용할 수 있습니다. 따라서 메모리 접근 비용이 줄어들어 좋을 것 같아 보이는데, memory hierarchy를 늘리는 것 역시 좋지 않습니다. 메모리를 여러개로 늘리게 되면 hardware area가 늘어납니다. 곧 비용의 증가로 이어집니다. 따라서 적절한 memory hierarachy 찾는 것이 중요하다고 볼 수 있습니다.
5.4.2 Spatial Reuse
Spatial reuse는 동일한 데이터를 여러개의 consumer(PE)들이 사용하는 것을 말합니다.
이 때에는 한 번 메모리에서 데이터를 읽은 후 여러개의 consumer에서 동시에 사용하게 됩니다.
Spatial Reuse를 사용하게 되면
- memory level에 접근하는 회수가 줄어들어 에너지 코스트가 줄어든다
- memory level로부터의 bandwidth가 줄어든다. 즉, PE가 쉬지 않고 연산을 하게 되어 performance가 증가한다
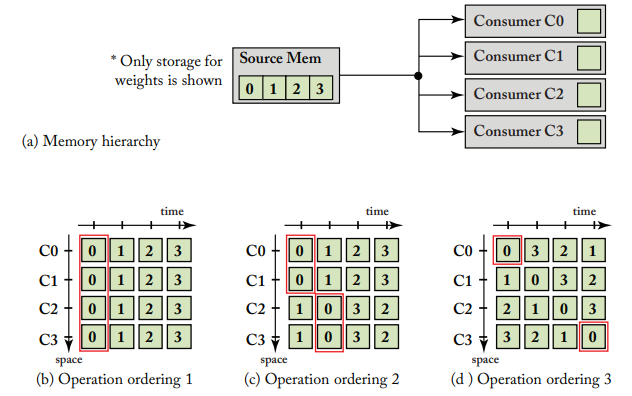
위의 그림을 보면 (a)는 4개의 데이터를 저장할 수 있는 Source Mem과 4개의 consumer C0~C3가 있습니다.
그리고 (b), (c), (d)에서는 각 reuse distance에 따라 어떻게 spatial reuse가 되는지를 보여줍니다.
(b), (c), (d)의 각 reuse distance는 아래와 같습니다.
- (b) : reuse distance = 0
- (c) : reuse distance = 1
- (d) : reuse distance = 3
Reuse distance가 0~1, 즉 reuse distance가 consumer storage capacity와 같거나 작은 경우에는 spatial reuse가 가능합니다. (b)의 경우 Source Mem으로 부터 0을 한 번 읽어 Consumer C0~C3까지 모두 사용하여 spatial reuse가 됩니다. 또한 (c)의 경우 역시 0번 time step에서 C0과 C1에서 함께 사용하고, 1번 time step에서 C2와 C3가 함께 사용해서 spatial reuse가 됩니다.
하지만 (d)를 보면 rreuse distance가 consumer sotrage 보다 커져 매 time step마다 C0~C3까지 새로운 데이터를 불러오게 되어 spatial reuse를 활용하지 못하는 것을 볼 수 있습니다.
temporal reuse와 마찬가지로 spatial reuse에서 역시 memory hierarchy를 늘리게 되면 어떻게 될까요?
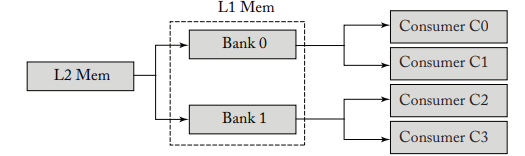
만약 L2 Mem과 Consumer 사이에 L1 Mem을 두게 된다면, memory 재사용과 관련해서는 L2에서 부터 고려가 되어야 합니다. L2에서 L1으로, L1에서 Consumer로 데이터가 전달되기 때문에 L2에서 부터 L1으로 데이터를 전송해 줄 때 재사용 될 데이터를 알맞게 전달해야 하기 때문에 고려해야 할 패턴이 더욱 많아지게 됩니다.
게다가 L1 Memory가 위와 같이 뱅크화가 된다면, L2 Mem에서 Bank0과 Bank1에 데이터를 전달해 줄 때 중복된 데이터가 전달 될 수도 있습니다. 이러한 경우가 잦아지게 되면 Bank로 나누는 이점이 사라지게 되므로 주의해야 합니다.
반면에 L2 Mem에서 Consumer C0~C3으로 직접 전달하게 되면 transfer cost가 커지게 되므로 위의 두 가지의 방법을 적절히 사용하는 것이 중요합니다. 이에 대한 내용은 5.9에서 다룬다고 합니다.
https://wh00300.tistory.com/246
Study note : Efficient Processing of Deep Neural Networks(3)
5.3 DNN HARDWARE DESIGN CONSIDERATIONS 5.3절에서는 DNN hardware design을 할 때의 고려사항에 대해서 설명합니다. DNN hardware를 design할 때 중요한 점으로는 "최적의 성능(performance, energy efficie..
wh00300.tistory.com
Reference
https://www.morganclaypool.com/doi/abs/10.2200/S01004ED1V01Y202004CAC050
Efficient Processing of Deep Neural Networks | Synthesis Lectures on Computer Architecture
Efficient Processing of Deep Neural Networks Vivienne Sze Massachusetts Institute of Technology Yu-Hsin Chen Massachusetts Institute of Technology Tien-Ju Yang Massachusetts Institute of Technology Joel S. Emer Massachusetts Institu
www.morganclaypool.com
'NPU' 카테고리의 다른 글
| Systolic array를 이용한 NPU에 대한 이해(3) : systolic array 실험 (4) | 2022.03.20 |
|---|---|
| Study note : Efficient Processing of Deep Neural Networks(5) (0) | 2021.12.15 |
| Study note : Efficient Processing of Deep Neural Networks(3) (0) | 2021.11.20 |
| Study note : Efficient Processing of Deep Neural Networks(2) (0) | 2021.11.13 |
| Study note : Efficient Processing of Deep Neural Networks(1) (3) | 2021.11.08 |



